2.目標変針に対する距離修正(1) 目標変針に影響される射距離誤差 目標の変針によって影響される射距離誤差の原因は次の2つに分析されます。 その一つは、射弾の飛行時中の目標運動による射距離誤差、即ち距離見越の変化によって生ずるもの。 (厳格に言えば測距費消時に対する修正も含まれます。) もう一つは、変距射法を行う場合に目標転舵を発見してその対策を講じるまでの飛翔時間中の変距誤測と変距量です。 測距射法では前者のみが影響を受けます。 (2) 飛行時中の射距離差の変化 一例として、40cm砲、射距離 25000m、的速 20ktの場合の修正量を計算すると次の表のようになります。
変距 (測距) の測定及び調定が無費消時で照尺距離を完全に実距離に並行させ得る場合には、上の表の値を目標転舵時に修正すれば、目標の定針時に同一の状況の弾着 (目標変針前の弾着と同一、という意味) が得られることになります。 しかしながら、実際にはこれらに相当の遅れ (費消時) がありますので、上記の修正量では不足するのが一般的です。 即ち、変距測定費消時中の照尺戦、実距離線の離隔量 (転舵に伴う誤測変距量) を修正する必要が出てきます。 一例として、40cm砲、射距離 25000m、変距測定費消時 30秒、的速 20ktの場合の費消時中の離隔量を計算すると次の表のようになります。
2つの修正量の関係は次図の様になります。 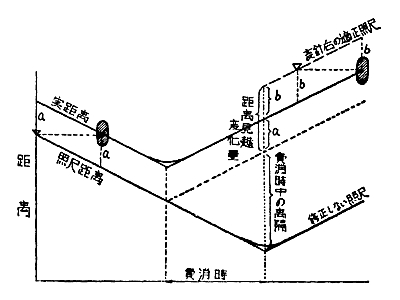 この2つの修正量を合計すると次の表のようになります。
(3) 修正法 目標の転舵に際しては、上の表のように 300 〜 600 の修正を行う必要があります。 しかしながら、目標がどれだけ転舵するのか、その角度を確実に知り得る方法はありませんから、ただ戦術的にそれを予想するだけです。 したがって、目標の変針を看破したならば直ちにこの予想転舵角度に対する修正を行うより他に方法はありません。 そして、転舵発見の前後には既に転舵の影響を受けた射弾が弾着しますので、転舵に対する修正が済んでいる場合には、修正を行わない (控える) か、あるいは適当な追加修正を行います。 最終更新 : 05/Jun/2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||